1.引例: 女士品茶
TM和MT两种方法做奶茶各四杯,给女士品尝,女士全部品尝出来了。她真的有分辨能力吗?
提出假设: 该女士没有分辨能力H_0
设A为女士正确分辨4杯TM:
推断结论:
(1) H_0不成立,即她又鉴别能力。
(2) H_0成立,但是概率为0.014的随机事件在一次试验中发生了。
2.相关概念
- 小概率事件原理
小概率事件在一次试验中几乎不可能发生。如果只做一次试验,该事件就发生了,就有理由怀疑试验前提的真实性。 - 检验统计量
用于假设检验问题的统计量。需要考虑: 总体是否正态分布;大样本还是小样本;总体方差是已知还是未知。
- 显著性水平
当原假设正确时人们却把它拒绝了的概率或风险。记为\alpha,通常取0.05或0.01或0.001。
3.假设检验的操作
- 基本步骤
1.提出原假设和备择假设
2.确定适当的检验统计量
3.规定显著性水平alpha
4.计算检验统计量的值
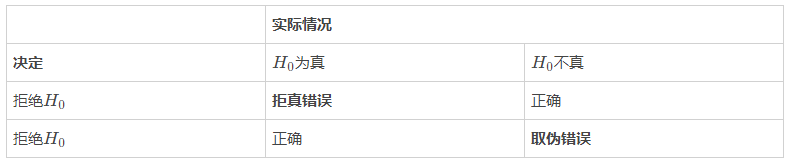
5.作出统计决策 - 两类错误
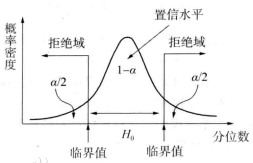
4.接受域和拒绝域
- 接受域: 原假设为真时允许范围内的变动,应该接受原假设。
- 拒绝域: 当原假设为真时又很小的概率出现,因而当统计量的结果落入这一区域便应拒绝假设,这一区域便称作拒绝域。
5.例题
某机床厂加工一种零件,根据经验知道,该厂加工零件的椭圆度近似服从美国正态分布,其总体均值为\mu_0=0.081mm,总体标准差为\sigma=0.025。进换一种新机床进行加工,抽取n=200个零件进行检验,得到的椭圆度为0.076mm。试问新机床加工零件的椭圆度的均值与以签有无显著差异? (\alpha=0.05)
H_0: \mu=0.081 H_1: \mu\not=0.081
\alpha=0.05 n=200
检验统计量:
决策: |\mu|=2.83>1.96,拒绝H_0
待完善
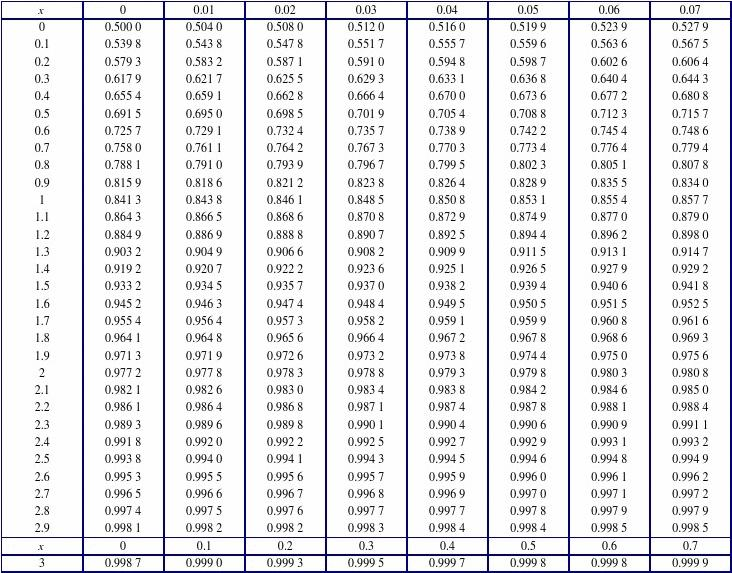
附: 标准正态分布表