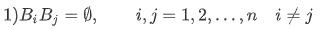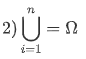1.条件概率与乘法公式

• 条件概率
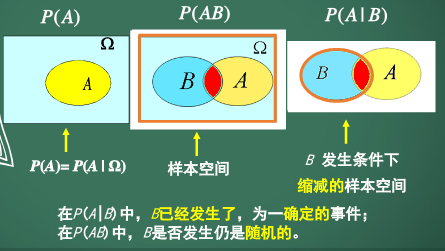
  事件B已发生的条件下，事件A发生的概率。记为P(A|B)。
  条件概率P(A|B)反映了事件的先后、主从关系。
  
• 条件概率公式
  \begin{equation}
  P(A|B)=\frac{P(AB)}{P(B)}
  \end{equation}
• 乘法公式
  \begin{equation}
  P(AB)=P(A|B)P(B)=P(B|A)P(A)
  \end{equation}
• 乘法公式推广
  \begin{equation}
  P(A_1A_2A_3)=P((A_1A_2)A_3)=P(A_1A_2)P(A_3|(A_1A_2))=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)
  \end{equation}

2.全概率公式（知因求果）

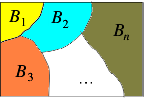
• 划分
  事件B_1,B_2,...,B_n为样本空间\Omega的自制件，且满足以下两个条件:
  
  
  则称B_1,B_2,...,B_n为样本空间\Omega的以组划分。
  
• 全概率公式
  P(B_i)>0,(i=1,2,3,...,n)，且A\subset\Omega，则有:
  
• 注意
  1.所求事件的概率受到多个因素的影响。
  2.分析清楚哪些事件对A有概率贡献，所以一定要注意把温杯时间组描述清楚。
  3.全概率公式中要用到的条件概率，一般是根据实际情况直接得到的。

3.贝叶斯公式（执果探因）

设随机试验E的样本空间为\Omega，A为E的事件，B_1,B_2,...,B_n为\Omega的一个划分，且P(A)>0\space P(B_i)>0\space (i=1,2,...,n)，则:

4.事件的独立性

• 两个事件独立
  • 定义1
    对于事件A、B，若有P(A)P(B)=P(AB)，则称事件A与B相互独立，简称独立。
  • 性质
    若事件A与B独立，那么A与\overline{B}，B与\overline{A}，\overline{A}与\overline{B}也独立。
  • 定理1
    如果四对事件A,B；A,\overline{B}；\overline{A},B；\overline{A},\overline{B}之中有一对相互独立，则另外三队也相互独立。
• 三个事件独立
  • 定义2
    如果事件A、B、C满足下列条件:
    1.P(ABC)=P(A)P(B)P(C)
    2.P(AB)=P(A)P(B)
    \space \space P(AC)=P(A)P(C)
    \space \space P(BC)=P(B)P(C)
    则称A、B、C是相互独立的。如果仅有2式成立，则称事件A、B、C是两两独立的。
    相互独立一定两两独立，反之不然。
• n个事件独立
  • 定义3
    设有n个事件A_1,A_2,A_3,...,A_n，若对其中任意m(2\le m\le n)个事件A_{i1},A_{i2},...,A_{im}都有P(A_{i1}A_{i2}...A_{im})=P(A_{i1})P(A_{i2})...P(A_{im})，则称事件A_1,A_2,...,A_n相互独立。
  • 定理2
    设n个事件A_1,A_2,...,A_n相互独立，则其中任意m(2\le m\le n)个事件也相互独立，将其中任意m(1\le m\le n)个事件换成对立事件后仍相互独立。
• 注意
  1.相互独立\not =互不相容
  2.相互独立则两两独立，反之不一定成立。

5.伯努利概型

• 特点
  1.试验可重复n次。
  2.每次试验只有两个可能结果A,\overline{A}。
  3.n次试验相互独立——每次试验结果与其它次试验无关。
  将n重伯努利试验中事件A出现k次的概率记为:
  \begin{equation}
  P_{\color{red}n}(k)
  \end{equation}
• 二项概率公式
  一般地，二项概率公式:
  \begin{equation}
  P(A)=p,\space P(\overline{A})=1-p=q
  \end{equation}
  n重伯努利试验中A恰好发生k次的概率:
  \begin{equation}
  P_n(k)=\color{red}{C_n^k}p^kq^{n-k}
  \end{equation}
  P_n(k)可视为二项式 (p+q)^n展开式中的一般想，故称为二项概率公式。