1. 问题描述
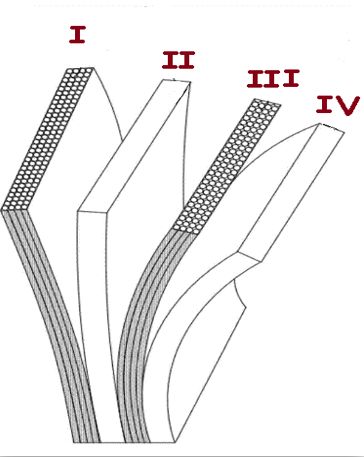
在高温环境下工作时,人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。
为设计专用服装,将体内温度控制在37的假人放置在实验室的高温环境中,测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期,请你们利用数学模型来确定假人皮肤外侧的温度变化情况,并解决以下问题:
(1) 专用服装材料的某些参数值由附件1给出,对环境温度为75、II层厚度为6、IV层厚度为5、工作时间为90分钟的情形开展实验,测量得到假人皮肤外侧的温度(见附件2)。建立数学模型,计算温度分布,并生成温度分布的Excel文件(文件名为problem1.xlsx)。
(2) 当环境温度为65、IV层的厚度为5.5时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47,且超过44的时间不超过5分钟。
(3) 当环境温度为80时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47,且超过44的时间不超过5分钟。
附件1 专用服装材料的参数值
| 分层 | 密度 (kg/m3) | 比热 (J/(kg·ºC)) | 热传导率 (W/(m·ºC)) | 厚度 (mm) |
|---|---|---|---|---|
| I层 | 300 | 1377 | 0.082 | 0.6 |
| II层 | 862 | 2100 | 0.37 | 0.6-25 |
| III层 | 74.2 | 1726 | 0.045 | 3.6 |
| IV层 | 1.18 | 1005 | 0.028 | 0.6-6.4 |
附件2 假人皮肤外侧的测量温度(原数据以表格形式给出)
2. 问题一
2.1. 问题分析
根据实验条件,可假设热量时垂直于皮肤方向进行传播的,从而将问题转化为一维热传导问题。根据能量守恒定理与热传导定律,建立一维热传导方程模型,确定边界条件,求出数值解。
2.2. 模型建立
2.2.1. 同一层内的热传导
假设材料时受热均匀的,且热传导沿垂直于复合材料外侧方向进行,可将三维空间问题转化为一维问题解决。
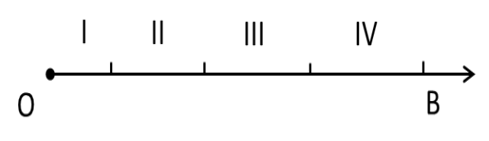
其中I、II、III、IV 分别为四层不同的材料; O点为外界点,即第一层材料的外层;B点为第四层材料的外侧。
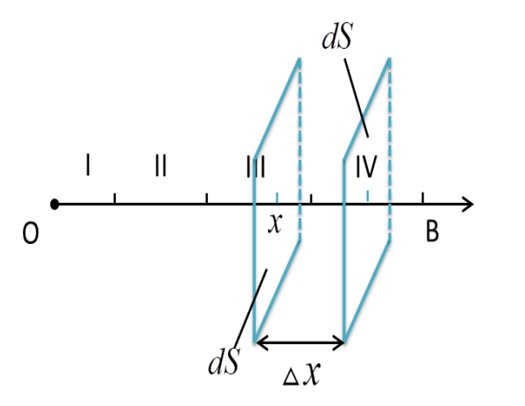
为了分别算出每一层的温度分布情况,我们在一维坐标轴上随机 插入两个面积为的微元, 如图所示。
根据能量守恒定律,在区域内各点的温度从时刻的温度改变为时刻的温度所吸收(或放出)的热量, 等于从时刻到这段时间内通过的热量和热源提供(或吸收)的热量之和,由于题中不含热源,故有如下关系:
根据傅里叶热传导定律,即物体在时间内流过面积为的热量与物体沿曲面法线方向的方向导数成正比,有:
其中为比例系数。因此,对于时刻到时刻通过处的热量,有:
根据热量公式,可得出时刻到时刻通过处的热量为:
其中为比热,为密度,且。
由于 ,有:
令,有:
至此,同层热传导数学模型建立完成。
2.2.2. 第I层左边界条件
根据牛顿冷却定律,从物体流到介质中的热量和两者的温差成正比,即:
其中为热交换系数,。
要分析流过第I层表面的热量,可从两个角度出发,即I层内部与外部,分别使用傅里叶定律与牛顿定律:
其中为外界与I层的热交换系数,为外界温度,为比例系数,通过上两式得:
2.2.3. 层与层得接触面
以第I层与第II层接触面为例,由于第I层厚度给定为,故,根据傅里叶热传导定律,有:
由于第I层与第II层直接接触,接触面温度相同,有:
其它接触面可作类似处理。
2.2.4. 第IV层右边界条件
由题目给出的数据,。与2.2.2得处理相似,可以从傅里叶定律与牛顿定律两方面确定:
由上式得:
其中为皮肤温度,为第四层与皮肤的热交换系数。
2.3. 数学模型
2.3.1. 第I层材料
2.3.2. 第II层材料
2.3.3. 第III层材料
2.3.4. 第IV层材料
2.4. 模型求解
2.4.1. 隐式差分格式
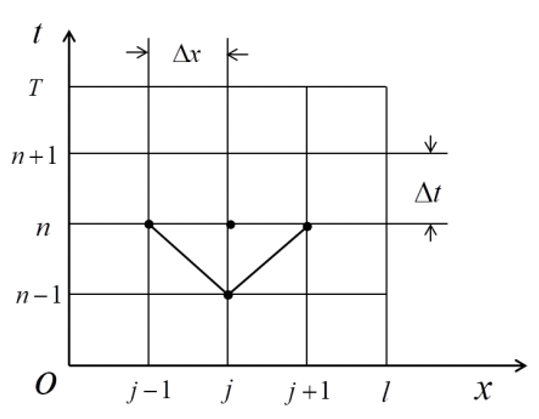
为方便计算,对区域进行离散化处理,采用隐式差分格式进行离散计算。隐式差分格式如图:
2.4.2. 每层材料内部
对于第层材料,有:
对方程左端采用向后差分格式,方程右端采用中心差分格式,有:
整理可得:
其中:
实现如下(以第I层为例):
r1 = k(1) * dt / (c(1) * rho(1) * dx * dx);
d1 = round(d(1) / dx + 1); %步数
for i = 2 : d1 - 1
A(i, i) = 1 + 2 * r1;
A(i, i - 1) = -r1;
A(i, i + 1) = -r1;
end
2.4.3. 左边界条件
初始条件:
此前求得的左边界条件:
对其进行离散化处理:
其中未知,。
整理可得:
根据2.4.2,有
联立可得:
实现如下:
A(1, 1) = 1 + 2 * r1 + 2 * dx * k_out * r1 / k(1);
b(1) = b(1) + 2 * dx * k_out * 75 * r1 / k(1); %随后一起解线性方程组,具体见完整代码
2.4.4. 右边界条件
与左边界条件同理,有:
其中未知。
实现如下:
A(d4, d4) = 1 + 2 * r4 + 2 * dx * k_skin * r4 / k(4);
b(N) = b(N) + 2 * dx * r4 * k_skin * 37 / k(4);
2.4.5. 各层材料接触面
对于第层与第层的接触面,有:
实现如下(以第I层与第II层接触面为例):
A(d1, d1 - 1) = -k(1) / dx;
A(d1, d1 + 1) = -k(2) / dx;
A(d1, d1) = -(A(d1, d1 - 1) + A(d1, d1 + 1));
2.4.6. 计算过程的实现
rho = [300, 862, 74.2, 1.18]; %密度
c = [1377, 2100, 1726, 1005]; %比热
k = [0.082, 0.37, 0.045, 0.028]; %热传导系数
%两个未知参数(需要估计)
k_out = 0;
k_skin = 0;
d = [0.0006, 0.006, 0.0036, 0.005]; %每层的厚度
dt = 1; %温度步长
dx = 0.1 * 10^(-3); %距离步长
r1 = k(1) * dt / (c(1) * rho(1) * dx * dx);
r2 = k(2) * dt / (c(2) * rho(2) * dx * dx);
r3 = k(3) * dt / (c(3) * rho(3) * dx * dx);
r4 = k(4) * dt / (c(4) * rho(4) * dx * dx);
N = round(sum(d) / dx + 1);
A = zeros(N); %等式左边(中间变量矩阵)
%左边界条件
A(1, 1) = 1 + 2 * r1 + 2 * dx * k_out * r1 / k(1);
%第I层
A(1, 2) = -2 * r1;
d1 = round(d(1) / dx + 1); %步数
for i = 2 : d1 - 1
A(i, i) = 1 + 2 * r1;
A(i, i - 1) = -r1;
A(i, i + 1) = -r1;
end
%第I层与第II层接触面
A(d1, d1 - 1) = -k(1) / dx;
A(d1, d1 + 1) = -k(2) / dx;
A(d1, d1) = -(A(d1, d1 - 1) + A(d1, d1 + 1));
%第II层
d2 = d1 + round(d(2) / dx);
for i = d1 + 1 : (d2 - 1)
A(i, i) = 1 + 2 * r2;
A(i, i - 1) = -r2;
A(i, i + 1) = -r2;
end
%第II层与第III层接触面
A(d2, d2 - 1) = -k(2) / dx;
A(d2, d2 + 1) = -k(3) / dx;
A(d2, d2) = -(A(d2, d2 - 1) + A(d2, d2 + 1));
%第III层
d3 = d2 + round(d(3) / dx);
for i = d2 + 1 : (d3 - 1)
A(i, i) = 1 + 2 * r3;
A(i, i - 1) = -r3;
A(i, i + 1) = -r3;
end
%第III层与第IV层接触面
A(d3, d3 - 1) = -k(3) / dx;
A(d3, d3 + 1) = -k(4) / dx;
A(d3, d3) = -(A(d3, d3 - 1) + A(d3, d3 + 1));
%第IV层
d4 = d3 + round(d(4) / dx);
for i = d3 + 1 : (d4 - 1)
A(i, i) = 1 + 2 * r4;
A(i, i - 1) = -r4;
A(i, i + 1) = -r4;
end
%右边界条件
A(d4, d4) = 1 + 2 * r4 + 2 * dx * k_skin * r4 / k(4);
A(d4, d4 - 1) = -2 * r4;
%温度
U = zeros(5401, N);
U(1, :) = 37;
%解线性方程,求出温度
for i = 1 : 5400
b = U(i, :)';
b(1) = b(1) + 2 * dx * k_out * 75 * r1 / k(1);
b(N) = b(N) + 2 * dx * r4 * k_skin * 37 / k(4);
b(d1) = 0;
b(d2) = 0;
b(d3) = 0;
U(i + 1, :) = A \ b;
end
2.4.7. 估计未知参数
由于与未知,需要进行估计。这里采用观察+手动二分法。
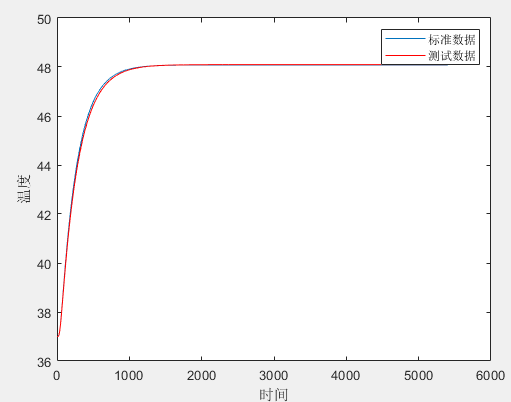
读取标准数据,绘制测试数据与标准数据的图像:
data = xlsread('D:\文件\数学建模\国赛培训\真题\2018-A-Chinese\CUMCM-2018-Problem-A-Chinese-Appendix.xlsx', 2);
figure
t = data(:, 1);
plot(t, data(:, 2))
xlabel("时间");
ylabel("温度");
hold on
plot(t, U(:, d4), 'r')
legend("标准数据", "测试数据");
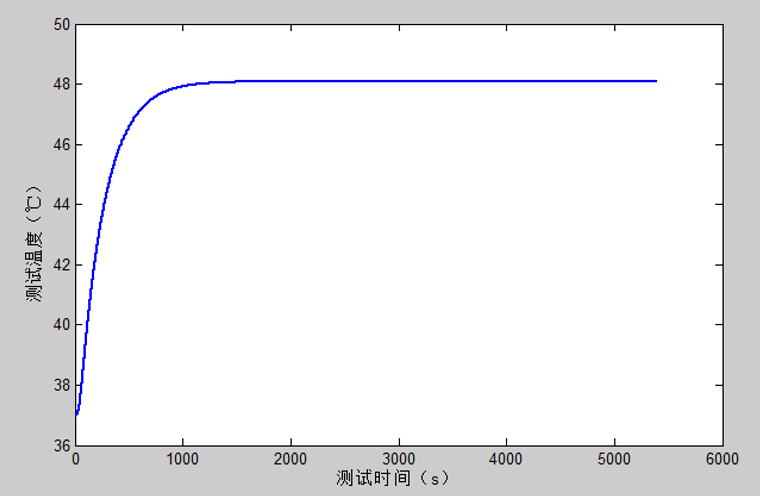
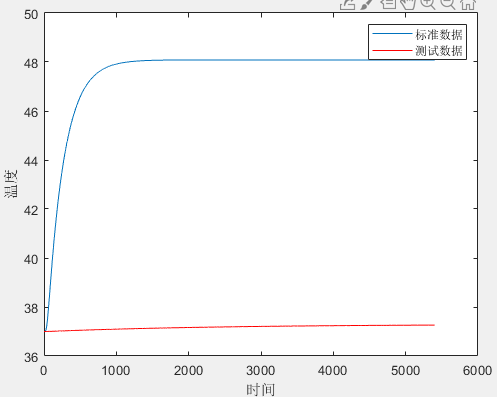
首先,根据题中所给数据绘制皮肤处温度随时间变化图像。
当时:
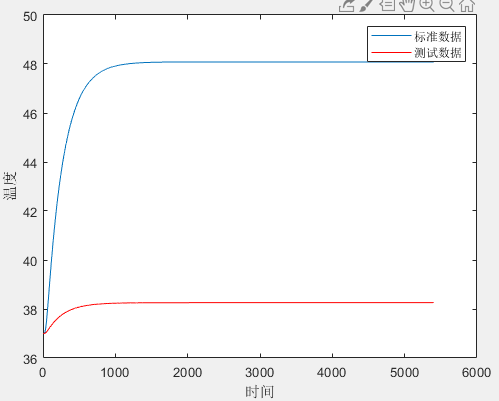
当时:
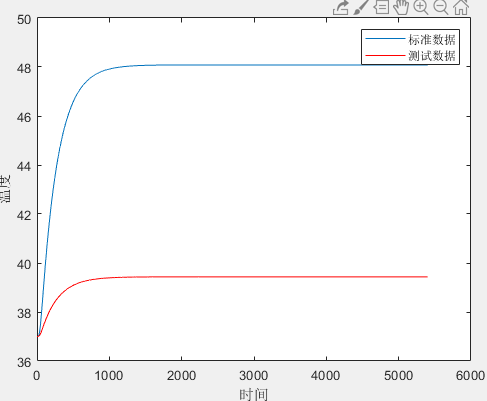
当时:
对比三个图像,可以作出如下猜测:
- 对上升阶段的影响更显著
- 对最终温度影响更显著
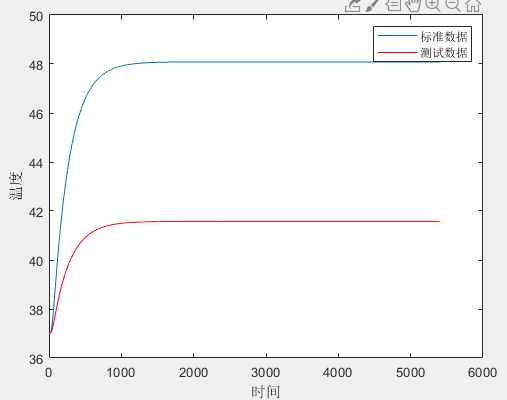
首先通过调整来调整最终温度使其接近理想值,当时:
当时:
随后尝试的情况,以此类推。
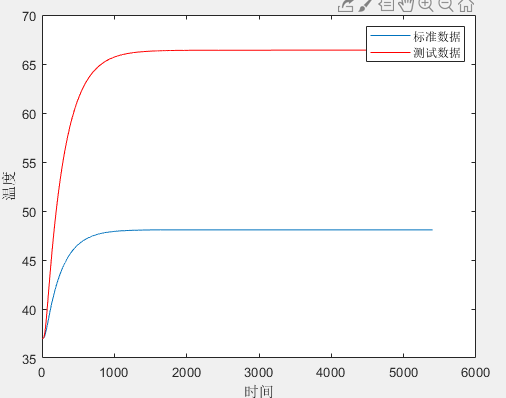
当时,曲线基本重合:
再对两个未知参数进行微调
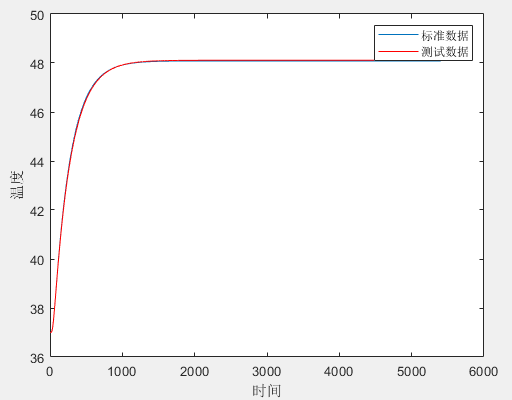
当时,曲线情况如下:
与标准数据重合度达到预期,此时,两个未知参数基本确定。
2.4.8. 得出结果
令,绘制图像
figure
mesh(U)
xlabel("位置");
ylabel("时间");
zlabel("温度");
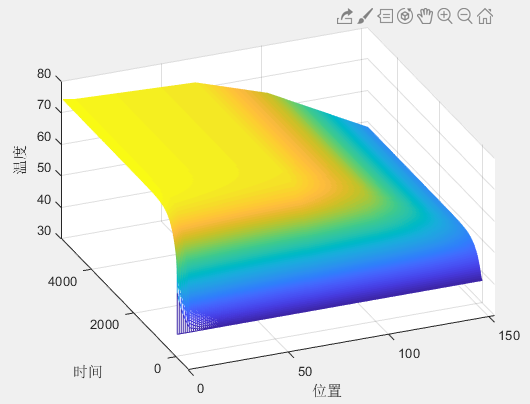
变量U情况如下:
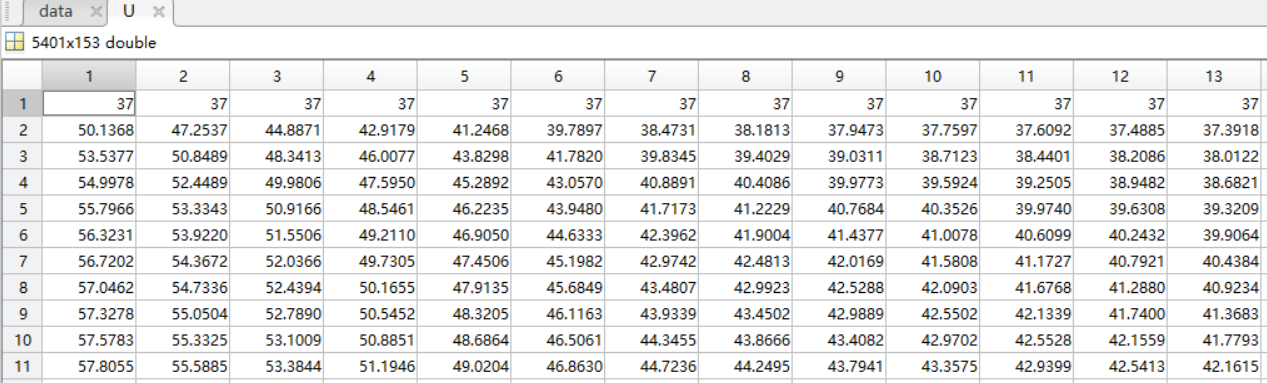
按照题目要求将变量保存为Excel表格:
xlswrite('D:\文件\数学建模\国赛培训\真题\2018-A-Chinese\problem1.xlsx', U);
2.4.9. 完整代码
rho = [300, 862, 74.2, 1.18]; %密度
c = [1377, 2100, 1726, 1005]; %比热
k = [0.082, 0.37, 0.045, 0.028]; %热传导系数
%两个未知参数(需要估计)
k_out = 106;
k_skin = 8.3;
d = [0.0006, 0.006, 0.0036, 0.005]; %每层的厚度
dt = 1; %温度步长
dx = 0.1 * 10^(-3); %距离步长
r1 = k(1) * dt / (c(1) * rho(1) * dx * dx);
r2 = k(2) * dt / (c(2) * rho(2) * dx * dx);
r3 = k(3) * dt / (c(3) * rho(3) * dx * dx);
r4 = k(4) * dt / (c(4) * rho(4) * dx * dx);
N = round(sum(d) / dx + 1);
A = zeros(N); %等式左边(中间变量矩阵)
%左边界条件
A(1, 1) = 1 + 2 * r1 + 2 * dx * k_out * r1 / k(1);
%第I层
A(1, 2) = -2 * r1;
d1 = round(d(1) / dx + 1); %步数
for i = 2 : d1 - 1
A(i, i) = 1 + 2 * r1;
A(i, i - 1) = -r1;
A(i, i + 1) = -r1;
end
%第I层与第II层接触面
A(d1, d1 - 1) = -k(1) / dx;
A(d1, d1 + 1) = -k(2) / dx;
A(d1, d1) = -(A(d1, d1 - 1) + A(d1, d1 + 1));
%第II层
d2 = d1 + round(d(2) / dx);
for i = d1 + 1 : (d2 - 1)
A(i, i) = 1 + 2 * r2;
A(i, i - 1) = -r2;
A(i, i + 1) = -r2;
end
%第II层与第III层接触面
A(d2, d2 - 1) = -k(2) / dx;
A(d2, d2 + 1) = -k(3) / dx;
A(d2, d2) = -(A(d2, d2 - 1) + A(d2, d2 + 1));
%第III层
d3 = d2 + round(d(3) / dx);
for i = d2 + 1 : (d3 - 1)
A(i, i) = 1 + 2 * r3;
A(i, i - 1) = -r3;
A(i, i + 1) = -r3;
end
%第III层与第IV层接触面
A(d3, d3 - 1) = -k(3) / dx;
A(d3, d3 + 1) = -k(4) / dx;
A(d3, d3) = -(A(d3, d3 - 1) + A(d3, d3 + 1));
%第IV层
d4 = d3 + round(d(4) / dx);
for i = d3 + 1 : (d4 - 1)
A(i, i) = 1 + 2 * r4;
A(i, i - 1) = -r4;
A(i, i + 1) = -r4;
end
%右边界条件
A(d4, d4) = 1 + 2 * r4 + 2 * dx * k_skin * r4 / k(4);
A(d4, d4 - 1) = -2 * r4;
%温度
U = zeros(5401, N);
U(1, :) = 37;
%解线性方程,求出温度
for i = 1 : 5400
b = U(i, :)';
b(1) = b(1) + 2 * dx * k_out * 75 * r1 / k(1);
b(N) = b(N) + 2 * dx * r4 * k_skin * 37 / k(4);
b(d1) = 0;
b(d2) = 0;
b(d3) = 0;
U(i + 1, :) = A \ b;
end
data = xlsread('D:\文件\数学建模\国赛培训\真题\2018-A-Chinese\CUMCM-2018-Problem-A-Chinese-Appendix.xlsx', 2);
figure
t = data(:, 1);
plot(t, data(:, 2))
xlabel("时间");
ylabel("温度");
hold on
plot(t, U(:, d4), 'r')
legend("标准数据", "测试数据");
figure
mesh(U)
xlabel("位置");
ylabel("时间");
zlabel("温度");
xlswrite('D:\文件\数学建模\国赛培训\真题\2018-A-Chinese\problem1.xlsx', U);

Dalao,请问为什么第四层那里的厚度是0.005啊,0.5毫米应该也不再范围里面啊
我当时就只写的第一问,题目给的0.5(这个过了很久了,我也忘了,可能答非所问了,抱歉)
谢谢Dalao!!!
恕我愚钝,能解释一下层与层之间哪里为什么是这样写吗?
%第I层与第II层接触面
A(d1, d1 – 1) = -k(1) / dx;
A(d1, d1 + 1) = -k(2) / dx;
A(d1, d1) = -(A(d1, d1 – 1) + A(d1, d1 + 1)) (这里为什么是这样写)
接触面的一侧向另一侧的热传递遵循傅立叶热传导定律,接触面本身左右温度相等。程序是根据前面的式子写的。(先粗略解释一下,如果您还有问题可以继续回复,我可以晚些时候重新研究一下
Dalao能不能来一篇2020数学建模国赛a题
我照着这篇的思路,搞不成
求Dalao赐教(就第一问就好了)
小小十块,不成敬意,还请笑纳
时隔久远,好像是网图,或者从哪个ppt里截出来的