0.问题简介
由于资源的有限性,当今世界各国都注意有计划地控制人口的增长,为了得到人口预测模型,必须首先搞清影响人口增长的因素,而影响人口增长的因素很多,如人口的自然出生率、人口的自然死亡率、人口的迁移、自然灾害、战争等诸多因素,如果一开始就把所有因素都考虑进去,则无从下手。因此,先把问题简化,建立比较粗糙的模型,再逐步修改,得到较完善的模型。
1.Malthus模型
- 模型假设
1.时刻的人口为
2.净相对增长率为
3.为连续变量 - 模型建立
按照Malthus理论,在到事件内人口增长量为,令,则得到微分方程:
若记起始时刻的人口为,则有:
- 模型求解
clear
clc
syms N(t) r N0
dsolve('DN = r * N', 'N(0) = N0')
解得
- 模型分析
如果,由(3)可知人口将以指数规律增长,当时,,这似乎不太可能。 - 模型检验
据估计1961年地球上的人口总数为,而在以后7年中,人口总数以每年2%的速度增长,这样,于是:
这个公式非常准确地反映了在1700—1961年间世界人口总数。因为这期间地球上的人口大约每35年翻一番,而上式断定34.6年增加一倍。但是,后来人们以美国人口为例,用马尔萨斯模型计算结果与人口资料比较,却发现有很大的差异,尤其是在用此模型预测较遥远的未来地球人口总数时,发现更令人不可思议的问题,如按此模型计算,到2670年,地球上将有36000亿人口。如果地球表面全是陆地(事实上,地球表面还有80%被水覆盖),我们也只得互相踩着肩膀站成两层了,这是非常荒谬的,因此,这一模型应该修改。
2.Logistic模型
- 模型假设
1.自然条件所能容许的最大人口数为
2.时刻的人口为
3.净相对增长率
4.为连续变量 - 模型建立
- 模型求解
clear
clc
syms N(t) N0 Nm r
dsolve('DN = r * (1 - N / Nm) * N', 'N(0) = N0')
解得:
- 模型分析
- 当,即无论人口初值如何,人口总数趋向于极限值
- 当时,,这说明是时间的单调递增函数,当取时,可由MATLAB作出图像:
clear
clc
ezplot('10 / (1 + (10 - 1) * exp(-0.1 * t))', [0, 100])
hold on
ezplot('10', [0, 100])
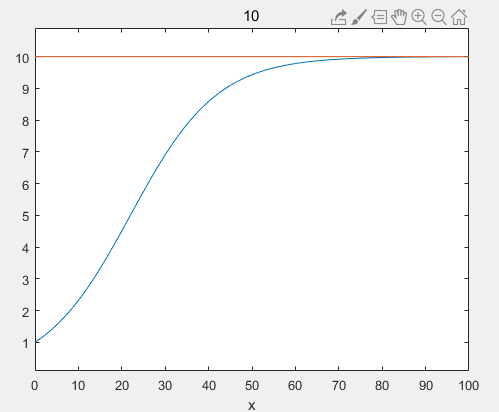
- 由于,所以当时,,单增;当时,,单减。即人口增长率由增变减,在处最大。也就是说在人口总数达到极限值一半以前是加速生长期,过这一点后,生长的速率逐渐变小,并且迟早会达到零,这是减速生长期。

你好,这是程序员自己的王国吗?我是偶然进来的.我连怎么注册都不知道
您好,这是我的私人博客,不开放注册的呢,抱歉哦。
嗯嗯,谢谢你的回复。我看了相关的用户,好像都是个人注册的网站,分享个人的文章。除了复制链接,有没有关注用户等途径来关注这里每个博主的精彩分享呢?
感谢您的喜欢,您可以用浏览器的收藏功能。如果您熟悉rss的话,可以订阅本站rss https://blog.tigerxly.com/rss 。
本站是我的私人博客,所有文章都是我写的,请问您是从哪里访问到这里的呢?
我在搜索人口预测模型时,多个链接下看到了您的模型。我试试您的回复。如果有同样感兴趣的朋友或“程序员朋友”,不知这样称呼是否合适,会进行分享的
已经使用你所说功能,可以避开很多无效干扰信息,谢谢你!