1.随机变量的分布函数
- 定义
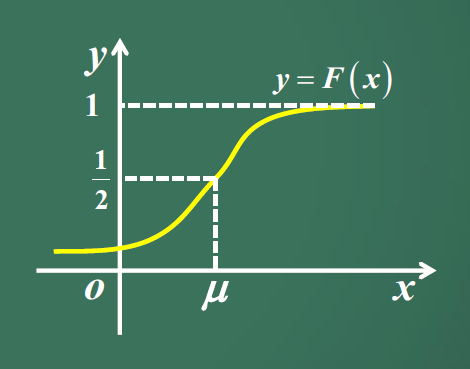
设$X$为一个随机变量,$x$是任意实数,函数
$$F(x)=P\lbrace X \leq x\rbrace (-\infty < x < +\infty)$$称为变量$X$的分布函数,也记为$F_X(x)$。 - 性质
分布函数的定义域为整个实数区间$R$。$P\lbrace a < X \leq b\rbrace = P\lbrace X\leq b\rbrace-\lbrace X\leq a\rbrace=F(b)-F(a)$
2.连续性随机变量的密度函数
- 定义
设$X$是一随机变量,$F(x)$是它的分布函数。如果存在一个非负函数$f(x)$,使对任意实数$x$,有:
$$F(x)=\int_{-\infty}^{x} f(x) d x$$则称随机变量$X$为连续型随机变量,并称$f(x)$为随机变量$X$的密度函数。 - 性质
- $\int_{-\infty}^{+\infty} f(x) d x=1$
- 对任意$a,b(a < b)$,有$P(a \leq X \leq b)=F(b)-F(a)=\int_{a}^{b} f(x) d x$。
- 在$F(x)$可导点$x$处,满足$\frac{d F(x)}{d x}=f(x)$。
3.均匀分布
- 定义
若:
$$X \sim f(x)=\begin{cases}
\frac{1}{b-a}&, x\in[a,b] \
0&,x\in(-\infty,a)\cup(b,+\infty)\end{cases}$$则称$X$服从$[a,b]$区间上的均匀分布,记为$X~U[a,b]$。 - 分布函数
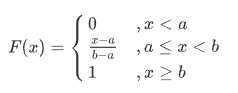
4.指数分布
- 定义
若:
$$X\sim f(x)=\begin{cases}
\lambda e^{-\lambda x}&,x>0\
0&,x\leq 0
\end{cases}$$则称$X$服从参数为$\lambda$的指数分布。记为$X\sim e(\lambda)$。 - 分布函数
$$X\sim F(x)=\begin{cases}
1-e^{-\lambda x}&,x>0\
0&,x\leq 0
\end{cases}$$
5.正态分布
- 定义
若
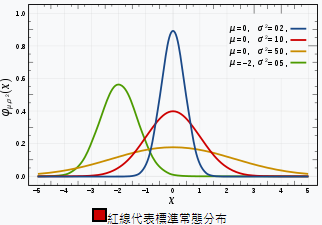
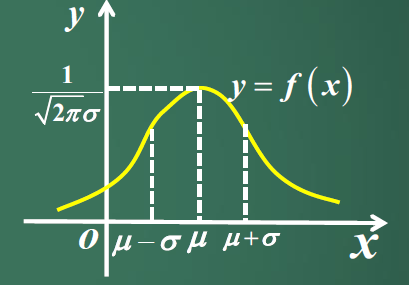
$$X \sim f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}},-\infty < x < +\infty$$其中$\mu,\sigma(\sigma>0)$为常数,则称$X$服从参数为$\mu,\sigma$的正态分布,记为$$X \sim N\left(\mu, \sigma^{2}\right)$$ - 性质
1.呈钟形,关于$x=\mu$对称,且在$x=\mu$处达到最大值$\frac{1}{\sqrt{2 \pi} \sigma}$。
2.$x=\mu\pm\sigma$处为拐点。
3.$\lim _{x \rightarrow \infty} f(x)=0$所以$X$轴为$f(x)$的渐近线。
4.固定$\sigma$,只改变$\mu$时,曲线形态不变,左右平移,固定$\mu$,只改变$\sigma$时,对称轴不变,曲线形态变尖或变扁。 - 分布函数
$$F(x)=\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{x} e^{-\frac{(t-\mu)^{2}}{2 \sigma^{2}}} d t$$当$\mu=0,\sigma^2=1$时,称$X$服从标准正态分布,记为$X \sim N(0,1)$其概率密度函数和分布函数分别为:
$$\varphi(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}} \quad \Phi(x)=\int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2}} d x$$ - 引理
若$X \sim N(0,1)$,则:
$$Y=\frac{X-\mu}{\sigma} \sim N(0,1)$$ - 定理
设$X \sim N(0,1)$,则:
$$P(a \leq x \leq b)=\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right)$$