本模型建立于2月6日,因为懒一直没写博文。本文未注明部分皆原创内容。
0.引言
近期,疫情肆虐,每个人都在盼望疫情早日得到控制。网上也出现了很多预测,其中有相当一部分预测是基于传染病模型的。由于本人是数学建模初学者,做不到精准的建模,本文通过SEIR模型研究传染病的发展趋势以及各种因素对传染病发展的影响。
1.传染病模型
传染病模型是传染病的基本数学模型,研究传染病的传播速度、空间范围、传播途径、动力学机理等问题,以指导对传染病的有效地预防和控制。常见的传染病模型按照传染病类型分为 SI、SIR、SIRS、SEIR 模型等,按照传播机理又分为基于常微分方程、偏微分方程、偏微分方程、网络动力学的不同类型。 (出处)
2.SEIR模型
SEIR模型是一种典型的传染病数学模型数学模型。在此模型中,将人群分为以下四类:
-
易感者(Susceptible)
易感者即尚未患病的人群,且有与病患接触的可能性。记为
S。 -
潜伏者(Exposed)
潜伏着即处于疾病潜伏期期的无症状模型。新型冠状病毒潜伏期也具有传染性。记为
E。 -
感染者(Infected)
感染者即被感染人群。记为
I。 -
康复者(Recovered)
康复者即痊愈病患。本模型认为康复者不会再次被感染。记为
R。
由于接触、隔离和治疗,这四类人群是可以相互转化的。为了简化模型,我们以固定的概率来体现转化。
3.模型建立
-
符号解释
符号 含义 易感者 潜伏者 感染者 康复者 每日每人接触到的人数 易感者被感染者感染的概率 易感者被潜伏者感染的概率 潜伏者转化为感染者的概率(潜伏期的倒数) 康复概率 总人数 -
模型详情
-
整理为迭代形式
4.代码详情
% seir_model_simulate.m
function seir_model_simulate()
clear();
N = 10000;
I = 1; %infectious
S = N - I; %susceptible
R = 0; %recovered
E = 0; %exposed
r = 20; %接触数
beta = 0.03; %被感染者传染
beta_1 = 0.02; %被潜伏着传染
alpha = 0.1; %潜伏期10天
gamma = 0.1; %康复概率
T = 1:150;
for i = 1:length(T) - 1
S(i + 1) = S(i) - r * (beta * I(i) + beta_1 * E(i)) * S(i) / N;
E(i + 1) = E(i) + r * (beta * I(i) + beta_1 * E(i)) * S(i) / N - alpha * E(i);
I(i + 1) = I(i) + alpha * E(i) - gamma * I(i);
R(i + 1) = R(i) + gamma * I(i);
end
plot(T,S,T,E,T,I,T,R);
grid on;
xlabel('天'); ylabel('人数')
legend('易感者','潜伏者','传染者','康复者')
end
5.结果与分析
使用上文代码中的数据,得到的结果如下图:
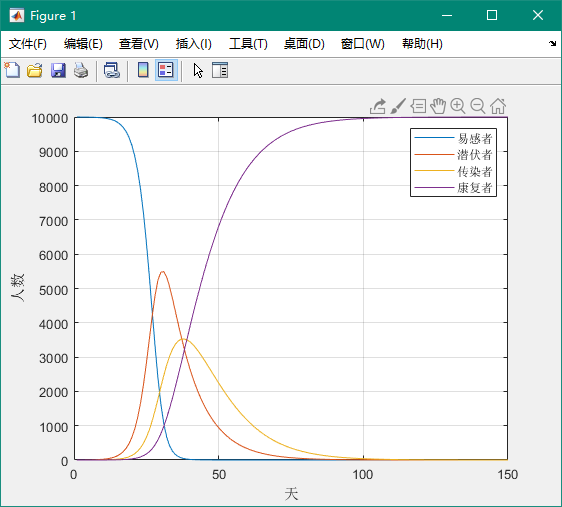
如果人们减少出行,做好防护,数据修改如下:
r = 3; %接触数
beta = 0.02; %传染概率
beta_1 = 0.01; %潜伏者传染概率
结果如下图:
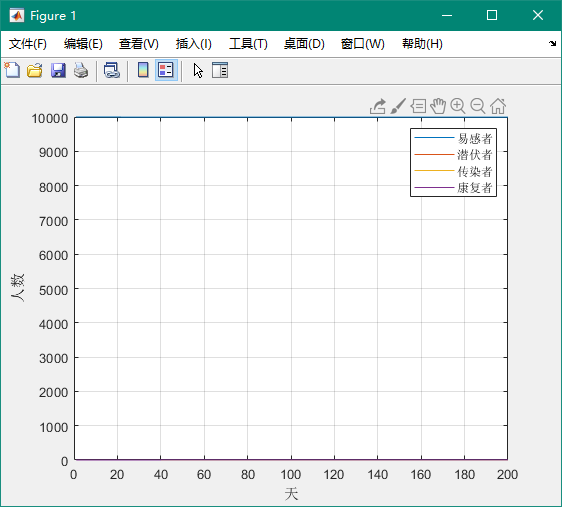
可以看到感染规模大幅减少,曲线基本消失。
虽然本模型有很多漏洞,并且有很多细节未顾及到,但是也可以看出少聚集,强防护是最好的预防。目前疫情有缓和的趋势,但是仍然不能掉以轻心。

就我自己加载不出图来吗
抱歉,本文年久失修,途中博客进行了改版更新,图源和公式显示都挂掉了,我会找时间修复
那大佬这个文章的图源还有吗,江湖救急
你急的话,可以右键审查元素。如果url是www.tigerxly.com…的话,把www改成blog即可。如果是外部图源挂了那我也无能为力了,抱歉。
想问一下博主,迭代公式是怎么推出来的啊,提点一下我这个笨蛋吧⌇●﹏●⌇
下标n代表第n时刻,实际上是将前面的一组式子离散化,方便编写程序求解。
好嘞 我再琢磨琢磨,蟹蟹博主啦!
博主 那个r是我们日常生活中每天接触到的人数还是 感染者在被确诊前接触到的人数呀 想了好久没想明白 希望能解答一下
不好意思之前看到您的评论本打算回的,后来忘记了,抱歉没有及时帮到您。这里的r指的是每个人在一天之内接触到的人数,就是你说的前者。
博主,红色部分是要自己取数字换上去吗
matlab运行代码显示
function seir_model_simulate()
↑
Error: Function definition not supported in this context. Create functions in code
file.
新建
.m文件来写函数,不要直接复制到命令行执行