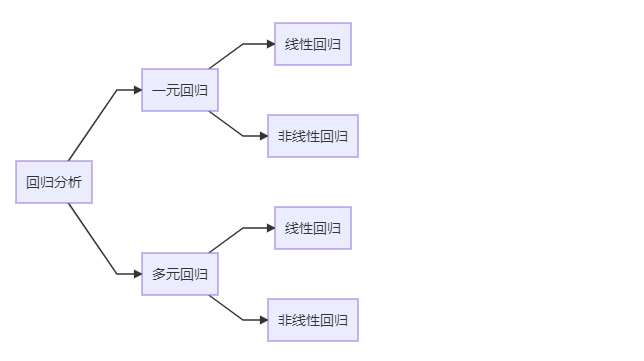
1.关于回归分析

• 任务

1. 从一组样本数据出发，确定变量之间的数学关系式。
2. 对这些关系式的可信程度进行各种统计检验，并从影响某一特定变量的诸多变量中找出哪些变量的影响显著，哪些不显著。
3. 利用所求的关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精确程度。

• 分类
  

2.一元线性回归模型

• 总体回归函数
  $$Y_{t}=\beta_{0}+\beta_{1} X_{t}+u_{t}$$
  $u_{t}$是随机误差项，又称随机干扰项，飞鹰味蕾如方程式的其它各种因素对$Y$的影响。
• 样本回归函数
  $$\hat{Y}{t}=\hat{\beta}{0}+\hat{\beta}{1} X{t}(t=1, 2, 3, \cdots, n)$$
  $e_t=Y_t-\hat{Y}_t$成为残差，与总体误差项$\mu_t$对应，$n$为样本容量。
• 样本回归函数与总体回归函数的区别

1. 总体回归线是未知的，只有一条。样本回归线是根据样本数据拟合的，每抽取一组样本，便可以拟合一条样本回归线。
2. 总体回归函数中的$\beta_0$和$\beta_1$是未知的参数，表现为常数。而样本回归函数中的$\hat{beta}_0$和$\hat{beta}_1$是随机变量，其具体数值随所抽取的样本观测值不同而变动。
3. 总体回归函数中的$u_t$是$Y_t$与未知的总体回归线之间的纵向距离，它是不可直接观测的。而样本回归函数中的$e_t$是$Y_t$与样本回归线之间的纵向距离，当根据样本观测值拟合出样本回归线之后，可以计算出$e_t$的具体数值。

未完待续