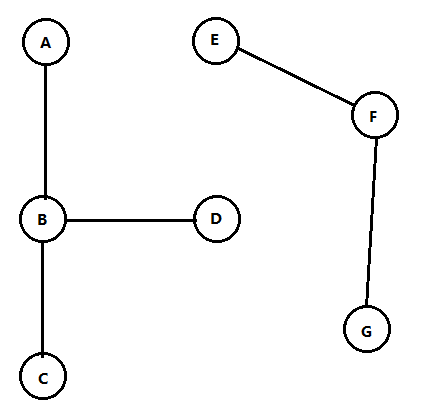
1.无向图的连通分量

直接说概念有点抽象，直接举例子：（如图所示）

如果对上图进行遍历，无论采用何种遍历方式，都会遍历两轮，形成{A,B,C,D}与{E,F,G}两个点集。实质上是对两个点集构成的的两个“子图”进行遍历，这两个“子图”就是该非连通图的两个连通分量。
求一个图的连通分量个数很简单，对每个点进行DFS或BFS，边遍历便标记，完成一次遍历计数器加一即可，具体见上一篇博客的HDU1241，本文就不给出代码了。

2.生成树

如果连通图 G的一个子图是一棵包含G 的所有顶点的树，则该子图称为G的生成树(SpanningTree)。常用的生成树算法有DFS生成树、BFS生成树、PRIM 最小生成树和Kruskal最小生成树算法。

3.关节点和重连通分量

• 关节点和重连通分量的定义
  在一个图中，如果删除一个点以及所有与之关联的边后，该图的一个连通分量变为多个连通分量，则这个点就是这个图的一个关节点，一个没有关节点的连通图成为重连通图。
• 查找关节点
  一个点如果是关节点，那么它满足以下两个充要条件：
  1)如果该点是图的DFS生成树的根节点，则该点有多个子树是该点未关节点的充要条件。
  2)如果该点是图的DFS生成树的其它非叶子节点，则该点存在一个子树不指向其祖先是该点是关节点的充要条件。
  也就是说，如果删除一个点其DFS生成树变为了森林，那么该点就是关节点。通常我们用如下DFS算法求解关节点：

DFS查找关节点（当前节点）{
    当前DFS深度加一；
    标记为已访问；
    记录当前节点DFS深度为其DFS到达点的最小深度；
    记录当前节点DFS深度；
    对每一个与之相邻的点{
        如果相邻点没被访问{
            DFS查找关节点（相邻点）；
            如果相邻点DFS到达点的最小深度小于当前节点DFS到达点的最小深度
                相邻点DFS到达点的最小深度为当前节点DFS到达点的最小深度；
            如果相邻点DFS到达点的最小深度大于等于当前节点DFS深度
                当前节点为关节点；
        }
        如果不是，且相邻点DFS深度小于当前节点DFS到达点的最小深度
            相邻点的DFS深度为当前节点DFS到达点的最小深度；
            // 因为此时相邻点是当前节点的祖先
    }
    记录当前节点DFS到达点的最小深度；
}

注意，上面的伪代码并没有判断根节点的情况，需要另外判断。伪代码已经很详细了，本文不会放出求关节点的详细代码了。

4.强连通分量

在有向图中，若任意两个顶点都有路径相通，则称该有向图为强连通图。一个有向图的极大强连通子图为该图的强连通分量。求强连通分量的方法主要有Tarjan算法和Kosaraju算法。教材中没有，考试不要求，日后再对两个算法作详细解释。

总提纲：《数据结构》期末提纲小结