1.图的简介
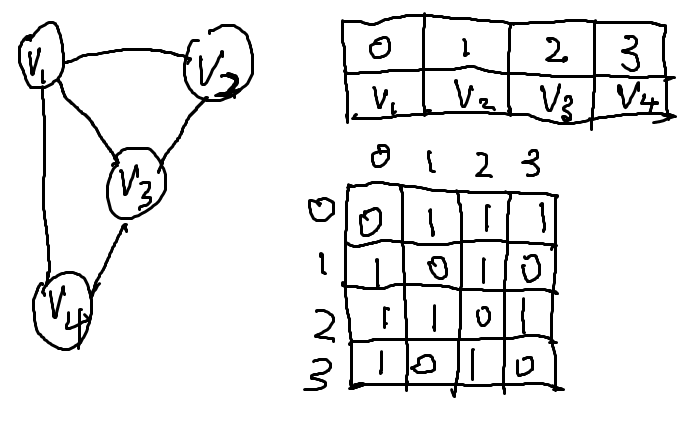
图(Graph)是表示物件与物件之间的关系的数学对象,是图论的基本研究对象。一个不带权图中若两点不相邻,邻接矩阵相应位置为0,对带权图(网),相应位置为∞。对于一个拥有n个顶点的无向连通图,它的边数一定多于n-1条。若从中选择n-1条边,使得无向图仍然连通,则由n个顶点及这 n-1条边(弧)组成的图被称为原无向图的生成树。(百度百科)
2.有向图与无向图
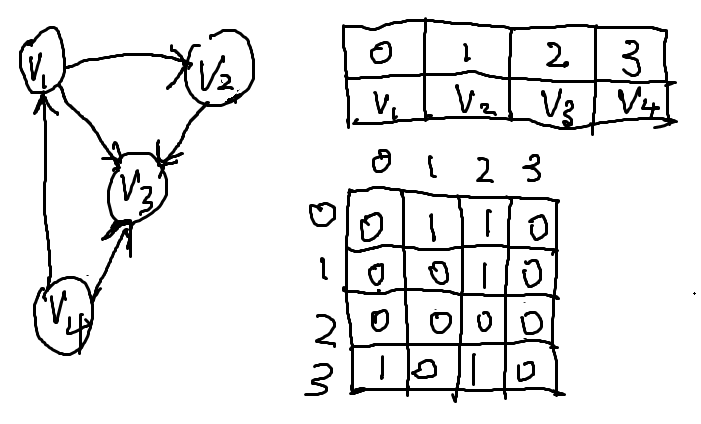
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,与一个节点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。
3.图的邻接矩阵
设有图G=(V,E),图中有n个顶点,可用两个数组表示这个图,一个一维数组存储图中顶点信息,一个二维数组存储图中的边或弧的信息,该二维数组成为邻接矩阵。对于一个有n个顶点的图,其邻接矩阵是一个nxn的方阵,定义为:Arc[i][j]=1,若(vi,vj)∈E或<vi,vj>∈E,反之等于0。若图带有边权,则邻接矩阵中存储权值。如图所示,是无向图图的邻接矩阵表示法:
如图是有向图的邻接矩阵表示法:
4.图的邻接表
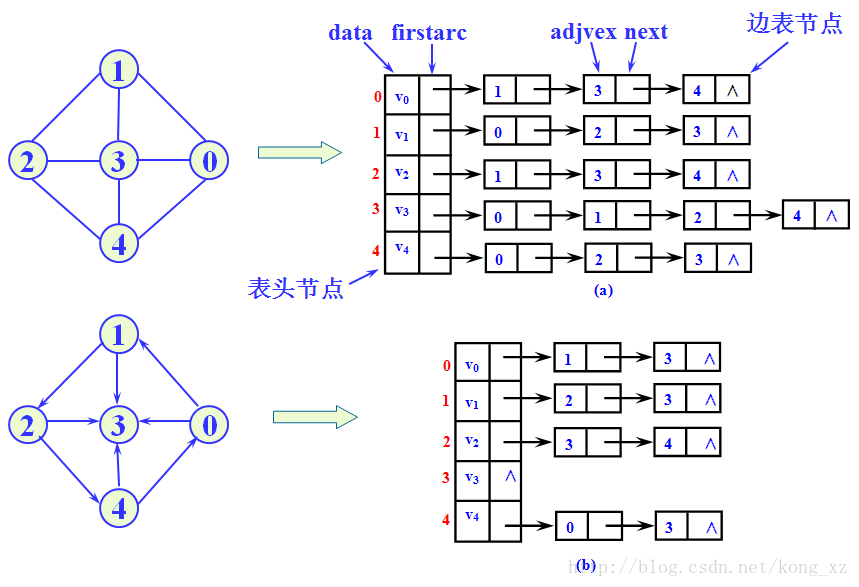
图的邻接表存储方法是一种顺序与链式相结合的存储方法。在邻接表中,对图中每个顶点建立一个单链表,第i个单链表中的节点表示依附于顶点i的边(对有向图是以顶点i为尾的边)。每个单链表上附设一个表头节点。其中,表节点由三个域组成,adjvex指示与顶点i邻接的点在图中的位置,nextarc指示下一条边或弧的节点,info存储与边或弧相关的信息,如权值等。表头节点由两个域组成,data存储顶点i的名称或其他信息,firstarc指向链表中第一个节点。(摘自这里,侵删)如图是图的邻接表:
5.图的存储实现
- 邻接矩阵
#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define M 1000000007
using namespace std;
typedef long long LL;
const int maxn = 1e2+6;
template <class T>
class graph
{
public:
graph(); //构造
~graph(); //析构
void create(); //创建
void print_list(); //输出邻接矩阵
private:
map<T,int> vertex; //顶点信息
int arc[maxn][maxn]; //邻接矩阵
int ver_num,arc_num; //顶点个数与边的个数
};
template <class T>
graph<T>::graph() //归零邻接矩阵,下同
{
memset(arc,0,sizeof(arc));
ver_num = 0;
arc_num = 0;
}
template <class T>
graph<T>::~graph()
{
memset(arc,0,sizeof(arc));
ver_num = 0;
arc_num = 0;
}
template <class T>
void graph<T>::create()
{
int v,a;
cout << "Input the number of vertexes: "; cin >> v;
cout << "Input the number of arcs: "; cin >> a;
ver_num = v;
arc_num = a;
for(int i = 0;i < ver_num;++i)
{
T tmp;
cout << "Input the data of the " << i + 1 << "th vertex: ";
cin >> tmp;
vertex[tmp] = i; //利用map结构作为哈希表
}
char flag;
cout << "Directed graph?(Y/n) "; cin >> flag;
if(flag == 'Y')
{
for(int i = 0;i < arc_num;++i)
{
T st,ed;
cout << "Input the starting point and the ending point of the " << i + 1 << "th arc: ";
cin >> st >> ed;
int sta = vertex[st];
int edd = vertex[ed];
arc[sta][edd] = 1;
}
}
else
{
for(int i = 0;i < arc_num;++i)
{
T st,ed;
cout << "Input the starting point and the ending point of the " << i + 1 << "th arc: ";
cin >> st >> ed;
int sta = vertex[st];
int edd = vertex[ed];
arc[sta][edd] = 1;
arc[edd][sta] = 1;
}
}
}
template <class T>
void graph<T>::print_list()
{
cout << ver_num << endl;
for(int i = 0;i < ver_num;++i)
{
for(int j = 0;j < ver_num;++j)
cout << arc[i][j] << " ";
cout << endl;
}
}
int main()
{
graph<int> G;
G.create();
G.print_list();
return 0;
}
- 邻接表
注意:邻接表代码没写打表,因为没意义,也因此无法系统debug,如果你发现以下代码有bug,请联系我。(菜鸡经常写bug)
#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define M 1000000007
using namespace std;
typedef long long LL;
const int maxn = 1e2+6;
struct node //邻接表节点
{
int loc; //图中位置
node* next;
};
template <class T>
struct vertex //节点结构体
{
T data; //数据
node* first_arc;
};
template <class T>
class graph
{
public:
graph(); //构造
~graph(); //析构
void create(); //创建图
private:
vertex<T>* ver[maxn]; //节点数组
int ver_num; //节点数
int arc_num; //弧数
};
template <class T>
graph<T>::graph() //构造方法
{
for(int i = 0;i < maxn;++i) //分配内存,初始化指针
{
ver[i] = new vertex<T>;
ver[i]->first_arc = NULL;
}
}
template <class T>
graph<T>::~graph() //析构方法
{
for(int i = 0;i < maxn;++i) //释放内存
{
while(true)
{
if(ver[i]->first_arc == NULL)
break;
node* p;
p = ver[i]->first_arc;
ver[i]->first_arc = p->next;
delete p;
}
delete ver[i];
}
}
template <class T>
void graph<T>::create()
{
int v,a;
cout << "Input the number of vertexes: "; cin >> v;
cout << "Input the number of arcs: "; cin >> a;
ver_num = v;
arc_num = a;
for(int i = 0;i < ver_num;++i)
{
T tmp;
cout << "Input the data of the " << i + 1 << "th vertex: ";
cin >> tmp;
ver[i]->data = tmp;
}
char flag;
cout << "Directed graph?(Y/n) "; cin >> flag;
if(flag == 'Y') //有向图情况
{
for(int i = 0;i < arc_num;++i)
{
T st,ed;
cout << "Input the starting point and the ending point of the " << i + 1 << "th arc: ";
cin >> st >> ed;
for(int i = 0;i < ver_num;++i)
{
if(ver[i]->data == st)
{
int edd;
for(int j = 0;j < ver_num;++j)
if(ver[j]->data == ed)
{
edd = j;
break;
}
node* new_node = new node; //头接
new_node->loc = edd;
new_node->next = ver[i]->first_arc;
ver[i]->first_arc = new_node;
// cout << ver[i]->first_arc->loc << endl;
break;
}
}
}
}
else //无向图情况
{
for(int i = 0;i < arc_num;++i)
{
T st,ed;
cout << "Input the starting point and the ending point of the " << i + 1 << "th arc: ";
cin >> st >> ed;
for(int i = 0;i < ver_num;++i)
{
if(ver[i]->data == st)
{
int edd;
for(int j = 0;j < ver_num;++j)
if(ver[j]->data == ed)
{
edd = j;
break;
}
node* new_node = new node;
new_node->loc = edd;
new_node->next = ver[i]->first_arc;
ver[i]->first_arc = new_node;
node* new_node_2 = new node;
new_node_2->loc = i;
new_node_2->next = ver[edd]->first_arc;
ver[edd]->first_arc = new_node_2;
break;
}
}
}
}
}
int main()
{
graph<int> G;
G.create();
return 0;
}
总提纲:《数据结构》期末提纲小结