版权声明：本文前两个图片出自这里，图片所属博主允许转载。本文其他部分若未说明即为原创。

1.最小生成树简介

在一给定的无向图G=(V,E)中，(u,v)代表连接顶点u与顶点v的边，而w(u,v)代表此边的权重，若存在T为E的子集且为无循环图，使得图中路径权值和最小，则此T为G的最小生成树。

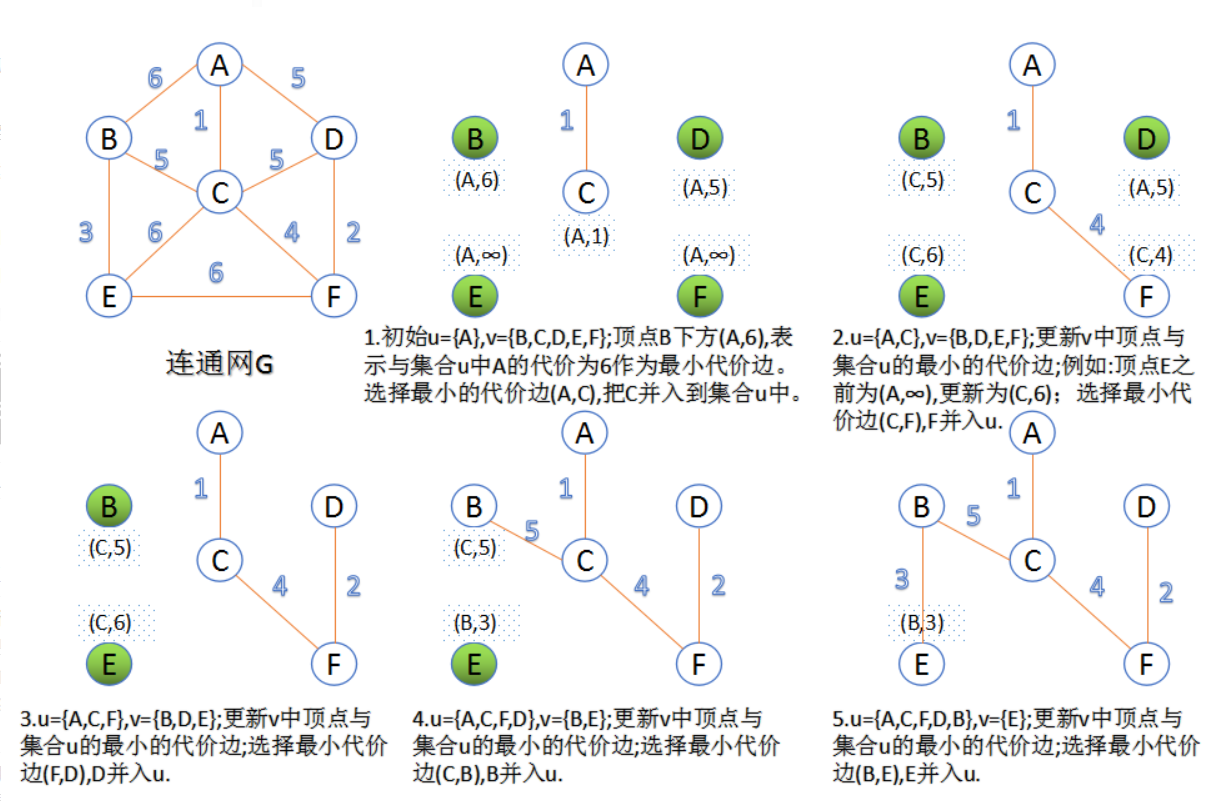
2.Prim算法

Prim算法相当于将点一个一个增加，算法解释比较抽象，直接看图即可：

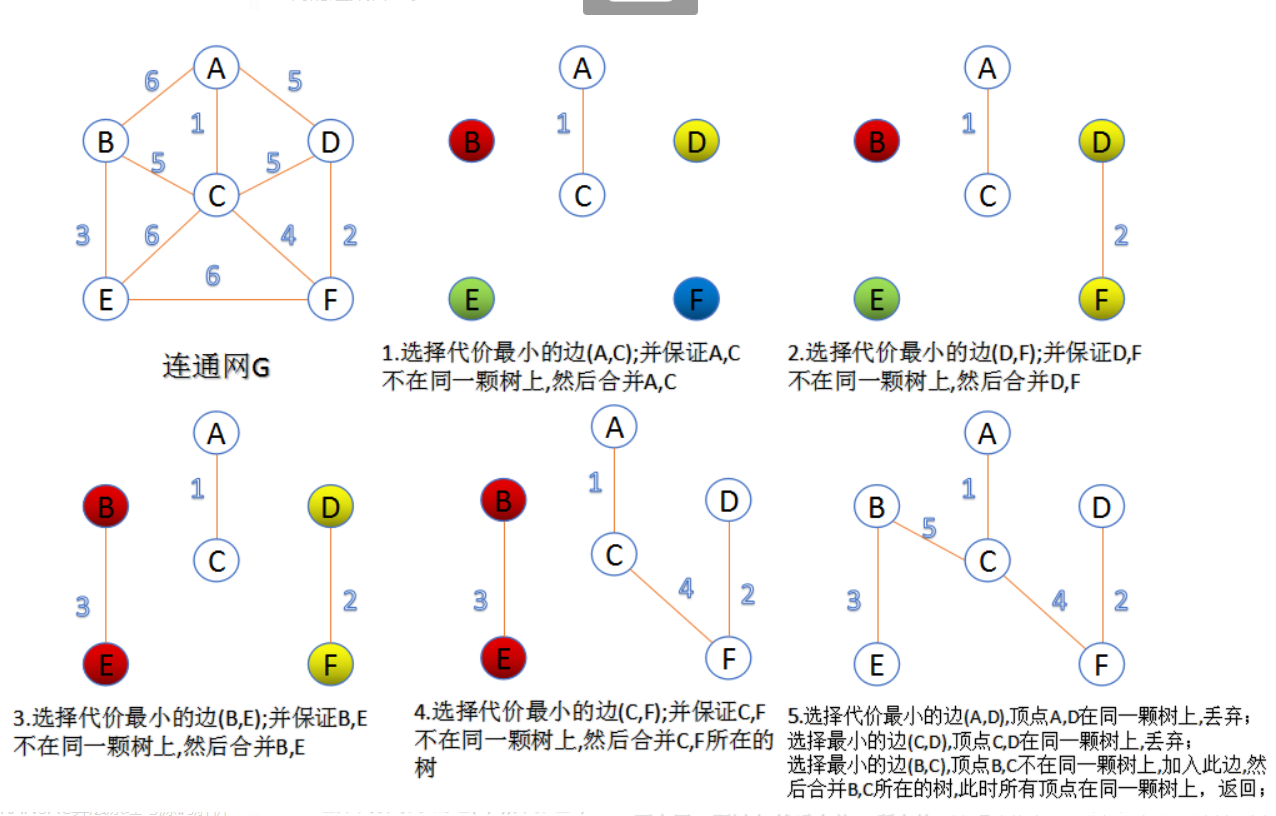
3.Kruscal算法

Kruscal相当于将边一个一个增加：

4.两种算法的实现

以HDU1301为例：

• 题意概括
  输入一个图，求这个图的最小生成树路径长之和。
• Prim算法求解思路
  将路径权值存入邻接表中，然后对每个点寻找路径最短邻接点并连接标记，直到连接到所有点。
• Prim算法实现

#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define M 1000000007
using namespace std;
typedef long long LL;
const int maxn = 35;

int adj[maxn][maxn];
bool vis[maxn];

void prim(int n)
{
    int sum = 0,cnt = 0,next;
    vis[0] = 1;
    while(cnt < n - 1)
    {
        int minn = INF;
        bool flag = false; //找到下一个点的标志
        for(int i = 0;i < n;++i)
        {
            if(!vis[i])
                continue;
            for(int j = 0;j < n;++j)
                if(!vis[j] && adj[i][j] < minn) //找到路径最小点
                {
                    minn = adj[i][j];
                    next = j;
                    flag = true;
                }
        }
        if(flag)
        {
            vis[next] = true;
            sum += minn;
            cnt++;
        }
    }
    printf("%d\n", sum);
}

int main()
{
    int n,tmp1,tmp2,m,l;
    char c[2];
    while(scanf("%d", &n) && n)
    {
        memset(adj,INF,sizeof(adj));
        memset(vis,false,sizeof(vis));
        for(int i = 0;i < n - 1;++i)
        {
            scanf("%s%d", c, &m);
            tmp1 = c[0] - 'A';
            for(int j = 0;j < m;++j)
            {
                scanf("%s%d", c, &l);
                tmp2 = c[0] - 'A';
                adj[tmp1][tmp2] = adj[tmp2][tmp1] = l;
            }
        }
        prim(n);
    }
    return 0;
}

• Kruscal算法求解思路
  存储每条边的信息，并且按权值从小到大排序，遍历这些边，利用并查集判断其两个端点是否连通，如果没有连通就连通他们，计算权值。由于用到并查集，不熟练的话实现难度比Prim算法大。
• Kruscal算法实现

#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define M 1000000007
using namespace std;
typedef long long LL;
const int maxn = 35;

struct node{int a,b,len;} arc[100]; //边结构体
int pre[maxn]; //并查集数组

bool cmp(node x,node y)
{
    return x.len < y.len;
}

void init()
{
    for(int i = 0;i <= 26;i++)
        pre[i] = i;
}

int find(int x)
{
    if(pre[x] != x)
        pre[x] = find(pre[x]);
    return pre[x];
}

void unit(int x,int y)
{
    int p = find(x), q = find(y);
    if(p != q)
        pre[p] = q;
}

int main()
{
    int n;
    while(scanf("%d", &n) && n)
    {
        init();
        int cnt = 0;
        for(int i = 0;i < n - 1;i++)
        {
            char c1[2],c2[2];
            int m,l;
            scanf("%s %d", c1, &m);
            for(int j = 0;j < m;j++)
            {
                getchar();
                scanf("%s %d", c2, &l);
                arc[cnt].a = c1[0] - 'A';
                arc[cnt].b = c2[0] - 'A';
                arc[cnt].len = l;
                cnt++;
            }
        }
        sort(arc,arc + cnt,cmp);
        int sum = 0;
        for(int i = 0;i < cnt;i++)
        {
            int x = find(arc[i].a);
            int y = find(arc[i].b);
            if(x != y) //如果不连通
                sum += arc[i].len;
            unit(x,y); //连通他们
        }
        printf("%d\n", sum);
    }
    return 0;
}

总提纲：《数据结构》期末提纲小结