本文翻译自英文，有少量改动
原文：https://codelabs.developers.google.com/codelabs/tensorflow-lab3-convolutions/#0
译者：van_fantasy

1. 引入：何为卷积

在本文中，你将会学习卷积的有关内容，并且了解到为何它在计算机视觉场景下表现得如此强大。在构建卷积神经网络时你必须在深度学习场景下使用卷积。

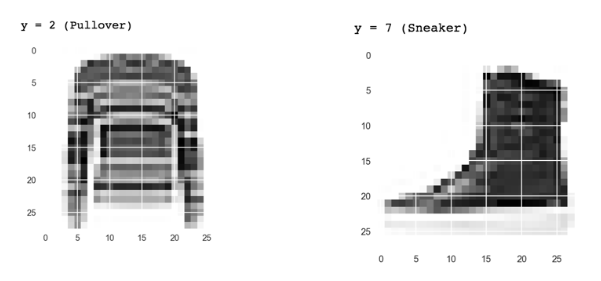
在上一篇文章中，你已经学习了如何使用Fashion MNIST数据集训练图像分类器，它比较准确，但是会有些明显的限制：图像必须为28*28的灰度图并且物品必须置于图片中央。

例如，Fashion MNIST数据集中有以下图片：

在这种情况下，你创建的深度神经网络（DNN）通过原始像素学习什么组成了毛衣、什么组成了靴子，但是请想想它能对下面这样的图片作分类吗？

毋庸置疑，这也是靴子，但是你的分类器会因为很多原因失效。首先，这张图不是28*28的灰度图，但更重要的是，你的分类器只是由向左摆放的靴子的原始像素点训练出来的，这并不是靴子的真实特征。为了解决这个问题，你得要使用卷积。

2. 卷积的使用

卷积可以被理解为图像的过滤器，它对图像进行处理，并提取共同性特征。在本文中，你将通过处理图像、提取特征等过程了解到卷积是如何运作的。

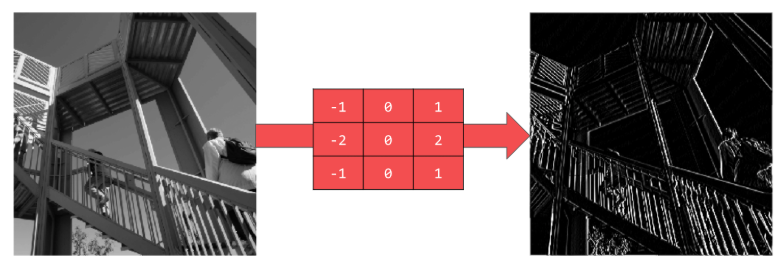
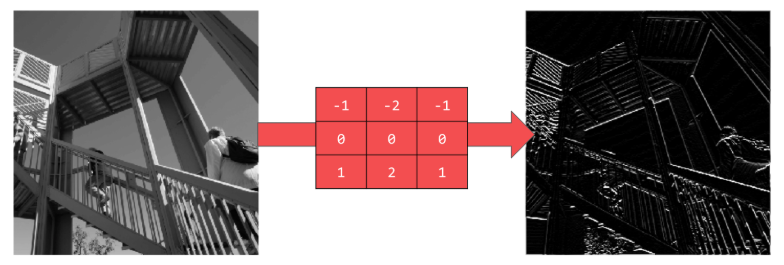
这个过程很简单，你只用扫描每一个像素点以及与之相邻的像素点，然后对这些像素点乘上过滤器中的权重。

举个例子，看看下面这张图：

在这里，我们指定了一个3*3的卷积矩阵。

当前像素点的值为192，然后你可以通过它周围的像素点的值乘上以及过滤器对应点的值计算出新的像素点的值。

下面，让我们通过构造一张2D灰度图的基本卷积来了解卷积的运作原理。

我们将用一张scipy的图片进行演示，它是一张有很多角度与线条的绝佳内置图片。

3. 开始编码

首先，引入需要用到的库，获取我们即将分析的图片：

import cv2
import numpy as np
from scipy import misc
i = misc.ascent()

然后，我们使用pyplot库来看看这个图片长什么样：

import matplotlib.pyplot as plt
plt.grid(False)
plt.gray()
plt.axis('off')
plt.imshow(i)
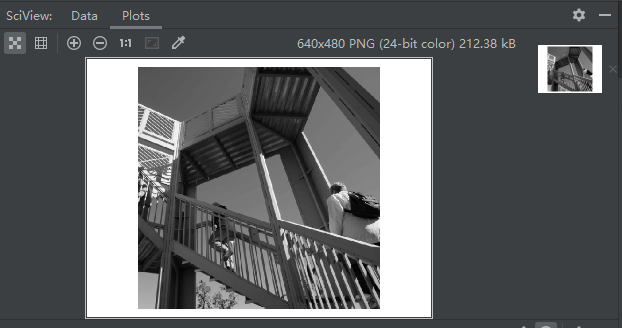
plt.show()

可以看到这是一个楼梯的图片，这里面有很多我们可以分离出来的特征，比如有很多竖直的线条。

这个图片被保存为一个numpy数组，所以我们可以直接复制数组来创建变换的图像，我们还可以获取图片的两个维度，以便之后进行循环。

i_transformed = np.copy(i)
size_x = i_transformed.shape[0]
size_y = i_transformed.shape[1]

4. 创建卷积

首先，我们构造一个3*3的卷积矩阵：

# 这个过滤器能很好地探测边缘
# 它构造了一个仅能通过边缘与直线的卷积
# 对不同的数据进行实验，获得有趣的效果
#filter = [ [0, 1, 0], [1, -4, 1], [0, 1, 0]] 
# 更多数据，可以拿去玩玩
filter = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1]]
#filter = [ [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]
# 如果过滤器中所有的数加起来不为0或1
# 你可能需要进行加权
# 比如你的权重为 1,1,1 1,2,1 1,1,1
# 加起来是10, 所以你要再加上0.1的权重
weight  = 1

现在，我们来计算输出的像素点。我们将遍历这个图像，预留一个像素的边缘，然后将当前像素点的相邻像素点乘上过滤器中定义的相应值。

所遍历到的像素点的左上角的像素点将被乘上过滤器左上节点的值，以此类推。随后我们将结果乘上权值，并确保最终结果在0和255之间。

最后，我们将数组的值加载到变换的图像中。

for x in range(1,size_x-1):
  for y in range(1,size_y-1):
      output_pixel = 0.0
      output_pixel = output_pixel + (i[x - 1, y-1] * filter[0][0])
      output_pixel = output_pixel + (i[x, y-1] * filter[0][1])
      output_pixel = output_pixel + (i[x + 1, y-1] * filter[0][2])
      output_pixel = output_pixel + (i[x-1, y] * filter[1][0])
      output_pixel = output_pixel + (i[x, y] * filter[1][1])
      output_pixel = output_pixel + (i[x+1, y] * filter[1][2])
      output_pixel = output_pixel + (i[x-1, y+1] * filter[2][0])
      output_pixel = output_pixel + (i[x, y+1] * filter[2][1])
      output_pixel = output_pixel + (i[x+1, y+1] * filter[2][2])
      output_pixel = output_pixel * weight
      if(output_pixel<0):
        output_pixel=0
      if(output_pixel>255):
        output_pixel=255
      i_transformed[x, y] = output_pixel

5. 检测结果

现在我们可以将图像显示出来，看看过滤的效果：

# 绘图，该图为512*512大小
plt.gray()
plt.grid(False)
plt.imshow(i_transformed)
#plt.axis('off')
plt.show() 

来分析一下下列过滤器的值，以及它们对图像的影响。

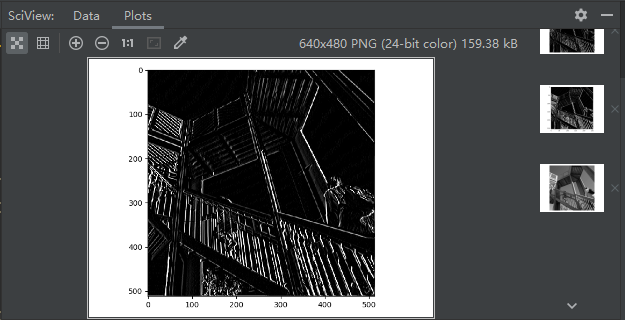
使用[-1,0,1,-2,0,2,-1,0,1]，我们会获得一些竖直的线条：

使用[-1,-2,-1,0,0,0,1,2,1]，我们会获得一些水平的线条：

可以继续探索不同的过滤器的值，也可以试试不同的过滤器大小，比如5*5或7*7。

6. 池化

在卷积之外，池化可以极大地帮助我们探测特征。池化的目标就是在保证检测到的特征的同时减少信息总量。

池化有不同的种类，本文介绍的是最大池化。

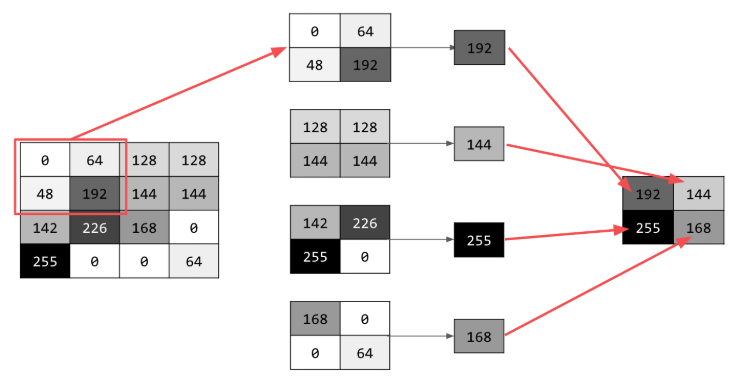
在此，我们对图像的像素点进行遍历，并记录该像素点的右、下、右下像素点。这4个点中的最大（所以交最大池化）点会被加载到新图像中，新图像只有原图像四分之一的大小。

7. 池化的实现

下面的代码展示的是(2,2)池化。你会发现它的运行结果只有之前的四分之一大小，并保留了原有特征。

new_x = int(size_x/2)
new_y = int(size_y/2)
newImage = np.zeros((new_x, new_y))
for x in range(0, size_x, 2):
  for y in range(0, size_y, 2):
    pixels = []
    pixels.append(i_transformed[x, y])
    pixels.append(i_transformed[x+1, y])
    pixels.append(i_transformed[x, y+1])
    pixels.append(i_transformed[x+1, y+1])
    pixels.sort(reverse=True)
    newImage[int(x/2),int(y/2)] = pixels[0]

# 绘图，大小变为了256*256
plt.gray()
plt.grid(False)
plt.imshow(newImage)
#plt.axis('off')
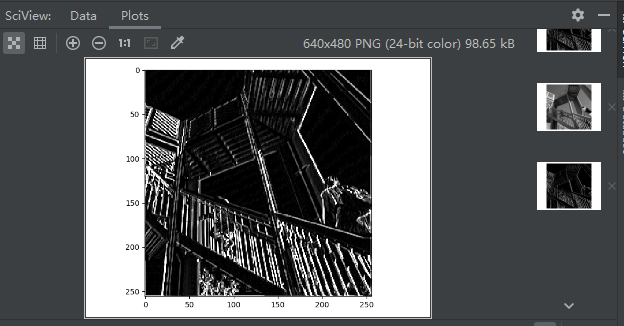
plt.show()

请注意坐标轴，该图为256*256大小，是原来的的四分之一，检测到的特征被强化的同时信息量减少了。

暑假应该会翻译一些机器学习方面的文章，也当是学习英语准备托福了。暑假应该也会写一些数学建模的笔记。